まだまだこの本の話を続けます。
■ [普及版]ジェネラティブ・アート―Processingによる実践ガイド
この本の各章で紹介されている「考え方」は、自分で作品を作っていこうとするときに、プログラミングとは別の部分での「基礎」となるものが多く、大変参考になりました。サンプルコードは、その考え方を言語で実装する場合の例になっています。私の場合、サンプルをp5.jsに移植しながら動かしていたのですが、その過程で、プログラムドローイングに必須の「基本テクニック」と呼べるようなものが、繰り返し出てきていることに気付きました。
個人的に、特に「知ってよかった」と感じたのは、
・sin、cosを使って座標を取る方法
・オブジェクト指向の基本
・noise関数の存在
の3つです。恐らく、プログラミングに慣れた人にとっては「何を今さら」な感じなのでしょうが、初学者が次のステップに進んでいくあたり、これらの要素を知っているか、使えるかというのは、その後の展開に大きな違いを生むのではないかと思います。
sin、cosで座標をとって図形を描く
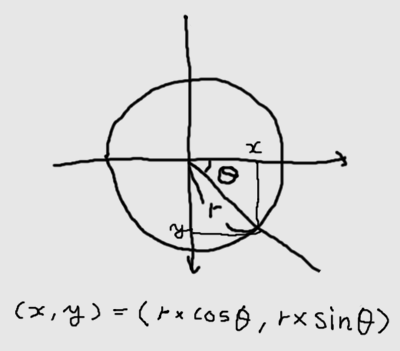
たしか、高校の数Iで出てきた三角関数の正弦定理と余弦定理。いわゆる「サイン(sin)」と「コサイン(cos)」。「原点を中心とする半径rの円と、x軸とθ度で交わり原点を通る直線とが交差する座標を求めよ」…って、なんのためにこんなワケのわからんムダなことさせるんじゃ、○ね、と当時は思っていたのですが、私にとっては「30年くらい後にプログラムで絵を描くため」であったことが判明しました。ムダとか言ってすみませんでした。
ゆくゆく物理シミュレーション的なことなどをやろうと思い立ってしまうと、きっと文字どおり「○ぬ」ほど難しい公式を使わなくてはならなくなるのでしょうが、簡単な絵を描くのであれば、下の対応さえ覚えておけば、結構いろいろなことができるようになります。
y軸の正方向が「下」になるのは、コンピュータで絵を描くときの伝統的なお約束です。
で、単位時間あたりに、この「θ」が同じ量ずつ変化するとき、同時に原点の位置がx軸上を等間隔に動いていけば、円と直線の交わる座標の軌跡は、いわゆる「サイン(コサイン)カーブ」と呼ばれる曲線を描きます。
var centY;
var x = 0;
var y = 0;
var r = 50;
var theta = 0;
function setup() {
createCanvas(600, 200);
centY = height/2;
background(230);
strokeWeight(1);
stroke(255);
line(0, 100, 600, 100);
drawCurve();
}
function drawCurve() {
for (var i=0; i<width; i++) {
strokeWeight(2);
stroke(0);
x++;
y = centY+r*sin(radians(theta));
theta+=2;
point(x, y);
}
}
原点の位置を動かさずに、θだけを増やしていくと、軌跡は原点を中心にrの半径を持つ円になります。で、実はこの方法を応用すると、円だけでなくさまざまな「正多角形」を、作り付けの関数に頼らずに描けるようになります。前のエントリでp5.jsとProcessingのコードの違いを説明するために作ったサンプルでは、その方法で3~8角形を描いています。
●[DEMO] 3~8角形までの図形をsinとcosで座標をとって描く(クリックすると別ウインドウが開きます)
function setup() {
createCanvas(600, 600);
background(255);
drawcross();
for (var h=3; h<9; h++) {
drawpolygon(h);
}
}
function drawcross() {
stroke(200);
strokeWeight(1);
for (var j=200; j<=400; j+=200) {
for(var i=150; i<=450; i+=150) {
line(i, j-70, i, j+70);
line(i-70, j, i+70, j);
}
}
}
function drawpolygon(peak) {
var centX = 150 * ((peak%3)+1);
var centY = 200 * floor(peak/3);
var peakX = centX;
var peakY = centY-55;
var lastpeakX = peakX;
var lastpeakY = peakY;
var anglestep = 360/peak;
for (var k=-90; k<=271 ; k+=anglestep) {
peakX = centX+cos(radians(k))*55;
peakY = centY+sin(radians(k))*55;
stroke(0);
strokeWeight(2);
line(lastpeakX, lastpeakY, peakX, peakY);
lastpeakX = peakX;
lastpeakY = peakY;
}
}
すべての図形は最後に定義している「drawpolygon」関数で描いているのですが、具体的にやっていることは、
・引数として図形の頂点数(3~8)をもらう
・スタート時のθは-90度(画面の一番上の頂点がくる場所)
・-90度から270度までを、360を頂点の数で割った分の角度ずつ回していき、その場所の座標をcosとsinでとる
・前の座標と新しくとった座標の間を直線でつなぐ
・一周したら関数での処理を終わる(一旦戻って次の図形へ)
という同じ処理になっています。この仕組みの応用と組み合わせで、いろんな絵が描けそうです。例えば、正5角形や6角形の頂点をすべて配列にとっておき、各点の間を線で結べば五芒星や六芒星も描けますね。また、原点を動かさず、半径(r)を段階的に増やしていくことで、軌跡は「渦巻き」状になります。
「ジェネラティブアート」では、第4章「円を描く間違った方法」で、このやり方を説明しており、応用として、半径と回転角の変化にランダム性を加えた「ノイズの多いらせん」の描き方を解説しています。
●[DEMO] “ノイズの多いらせん” powered by p5.js(クリックすると別ウインドウが開きます)
サンプルでは、リロードごとに100個のランダムならせんが画面上に描かれますが、らせんの数を減らしたり増やしたりすると、また違った感じのできあがりになります。
子どもが鉛筆やボールペンでグリグリと落書きをした感じですが、プログラムでこうした絵が作れるのって面白いですよね。
仕組みの「組み合わせ」を増やし「ランダム性」を洗練させていった結果が、以前紹介した「Wave Clock」のような「作品」になります。
●[DEMO] “Wave Clock” powered by p5.js(クリックすると別ウィンドウが開きます)
Wave Clockでは、見えない円の「半径」「原点」をなだらかに変化させつつ、その円周上を速度を変えて移動する点と、原点対称にある点とを、さらに変化する色の線で結んでいます。
シンプルな仕組みを多層に組み合わせ、そこに何らかの不確定要素(乱数とかノイズとか)を加えてやることで、毎回異なる、予想外の結果(絵)が出てくるというのが、ジェネラティブアートの面白さのひとつにあるのではないかと思います。
残る2つのテクニック「オブジェクト指向」「noise関数」については、そのうちまた別のエントリにしようと思います。




知ってよかった「p5.js」でのお絵描きテクニック3つ はコメントを受け付けていません