今年の3月に買ったこの本。
■ [普及版]ジェネラティブ・アート―Processingによる実践ガイド
当初、これに掲載されていた「Processing」用のサンプルプログラムを「p5.js」で動くように移植しつつ読み進めておりました。移植にあたって主に参考にしたのは、
■ p5.jsプログラミングガイド
こちらの本と、Githubのp5.js Wikiにあるこちらのエントリでした。
ざっくりまとめてしまうと、Processingのコードをp5.js用にする場合、
・キャンバスサイズを定義する「size」は「createCanvas」に書き直す
・「pushMatrix/popMatrix」から「push/pop」等、一部関数名が変更されているものがあるのでそれらを書き直す
・関数定義の「void」は「function」に書き直し
・「int」「float」「double」「boolean」「char」とかいった変数の型定義はできないので、とりあえず全部「var」にしておく
ひとまず、多次元配列やクラス定義を使っていないシンプルなProcessingコードなら、これだけやっておけばp5.jsで動くと思います。「ジェネラティブ・アート」に掲載されているサンプルのうち「Chapter 6 創発」までにあるものは、ほぼこれらと、
・クラス定義がある場合、「void class なんたら」を「function なんたら」に書き換え。メソッドを定義している場合は「なんたら.prototype.かんたら = function () {…}」を使ったJavascript方式で書き換え
でイケたように記憶しています。
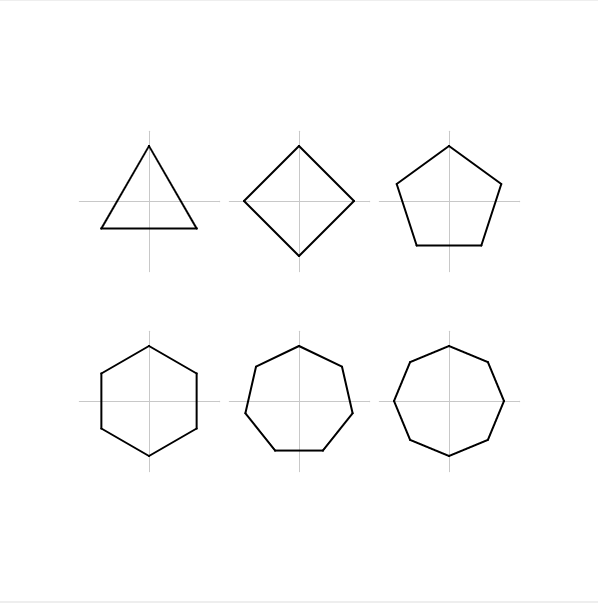
次のデモは自分で書いた「3~8角形までの図形をsinとcosで座標をとって描く」p5.jsのプログラムです。
●[DEMO] 3~8角形までの図形をsinとcosで座標をとって描く(クリックすると別ウインドウが開きます)
ソースコードがこちら。
function setup() {
createCanvas(600, 600);
background(255);
drawcross();
for (var h=3; h<9; h++) {
drawpolygon(h);
}
}
function drawcross() {
stroke(200);
strokeWeight(1);
for (var j=200; j<=400; j+=200) {
for(var i=150; i<=450; i+=150) {
line(i, j-70, i, j+70);
line(i-70, j, i+70, j);
}
}
}
function drawpolygon(peak) {
var centX = 150 * ((peak%3)+1);
var centY = 200 * floor(peak/3);
var peakX = centX;
var peakY = centY-55;
var lastpeakX = peakX;
var lastpeakY = peakY;
var anglestep = 360/peak;
for (var k=-90; k<=271 ; k+=anglestep) {
peakX = centX+cos(radians(k))*55;
peakY = centY+sin(radians(k))*55;
stroke(0);
strokeWeight(2);
line(lastpeakX, lastpeakY, peakX, peakY);
lastpeakX = peakX;
lastpeakY = peakY;
}
}
で、これをProcessingで動くように直すとこうなります。
void setup() {
size(600, 600);
background(255);
drawcross();
for (int h=3; h<9; h++) {
drawpolygon(h);
}
}
void drawcross() {
stroke(200);
strokeWeight(1);
for (int j=200; j<=400; j+=200) {
for(int i=150; i<=450; i+=150) {
line(i, j-70, i, j+70);
line(i-70, j, i+70, j);
}
}
}
void drawpolygon(int peak) {
int centX = 150 * ((peak%3)+1);
int centY = 200 * floor(peak/3);
float peakX = centX;
float peakY = centY-55;
float lastpeakX = peakX;
float lastpeakY = peakY;
float anglestep = 360/peak;
for (float k=-90; k<=271 ; k+=anglestep) {
peakX = centX+cos(radians(k))*55;
peakY = centY+sin(radians(k))*55;
stroke(0);
strokeWeight(2);
line(lastpeakX, lastpeakY, peakX, peakY);
lastpeakX = peakX;
lastpeakY = peakY;
}
}
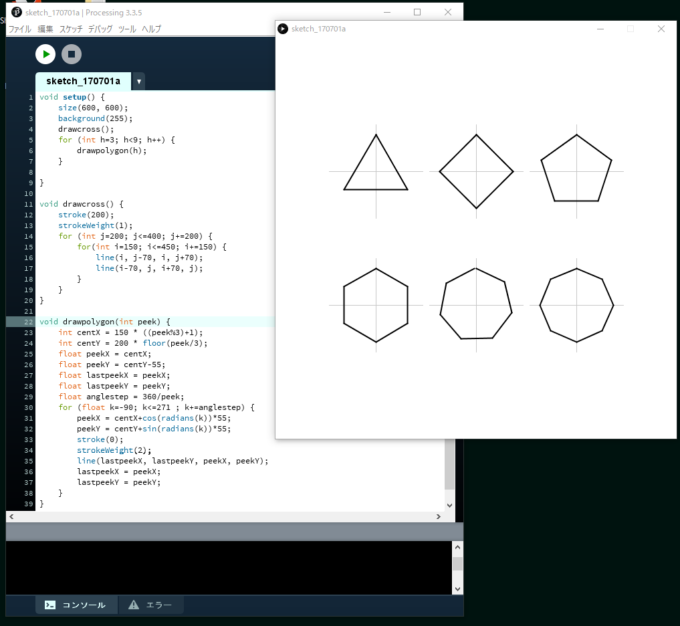
Processingで動かすと、こんなかんじでほぼ同じ結果が得られます。
「ほぼ同じ」というのは、計算精度の違いが影響して、Processingでは7角形の一番上の頂点位置が微妙にズレています。あくまでコード上の違いを比較する際のご参考までに。
まぁ、ほぼこんな感じでChapter 6までは進めたのですが、「Chapter 7 自律性」の「セルオートマトン」、「Chapter 8 フラクタル」については、若干手間取りました。結果的にフラクタルの「サトクリフ五角形」最終形については挫折してしまったのですが、それ以外のものについてはいちおう動かすところまでいきましたので、そのうちこちらで書きたいと思います。特に「セルオートマトン(CA)」は、これまでに見たCAフレームワークの中でも特に汎用性の高い、美しい作り方になっており、移植しながら感心しきりでした。



Processingからp5.jsへの移植は(難しいことしなければワリと)簡単 はコメントを受け付けていません