「次はフラクタルをゴニョゴニョする」と書いてからはやひと月半。既に街は師走の大詰めです。仕事以外もいろいろと忙しい年の瀬ですが、自分で自分に出した宿題を新年に持ち越さぬよう、粛々と書いていきたい所存です。
さて、「ジェネラティブ・アート―Processingによる実践ガイド」では、最終章でフラクタルのスケッチが2つ紹介されていました。
■ [普及版]ジェネラティブ・アート―Processingによる実践ガイド
「そういや、『フラクタル図形』っていろいろあるけれど、一般的な定義ってきちんと調べたことないな」と思いながらWikipediaをググってみたところ、次のように書かれておりました。
フラクタル(仏: fractale, 英: fractal)は、フランスの数学者ブノワ・マンデルブロが導入した幾何学の概念である。ラテン語 fractus から。 図形の部分と全体が自己相似になっているものなどをいう。
……
フラクタルの特徴は直感的には理解できるものの、数学的に厳密に定義するのは非常に難しい。マンデルブロはフラクタルを「ハウスドルフ次元が位相次元を厳密に上回るような集合」と定義した。完全に自己相似なフラクタルにおいては、ハウスドルフ次元はミンコフスキー次元と等しくなる。
ミ、ミンコフスキー次元?? ミノフスキー粒子みたいなもんでしょうか。なんか、よく分かんないですが「図形の部分と全体が自己相似」ってのは、よく聞きますね(^^;。あと、考案者であるマンデルブロの名前は、フラクタル画像の名称にも使われており超有名です。TEDでもプレゼンしてます。
「ジェネラティブ・アート」にあるフラクタルのスケッチは、いずれも再帰(ある処理の中から同じ処理を多重に呼び出す)の仕組みを内包しつつ、著者のアレンジが加わった面白いものなのですが、今回はひとまず、より古典的だったり有名だったりする4つのスケッチをp5.jsで動かしてみます。
何はなくとも「マンデルブロ集合」
フラクタルといえばマンデルブロ。マンデルブロといえばフラクタル。まずは、子どものころからの憧れだった「マンデルブロ集合」をp5.jsで描きたいっ!
…えーと、とりあえず定義の式が分からないと話になりませんから、ちょっと調べてみましょう。
…あー…。な、なるほどね。オタフクソースね。じゃなくて、フクソスーね。知ってる知ってる。プラスマイナスとか虚数のiとかが付くアレね。
…えー、無理です。コードに起こすどころか、式の意味さえ理解できません。orz ムネンアトヲタノム
ド文系としては、自分で式を理解するのを諦めて、こちらの方が公開してくださっているProcessing向けのソースを使わせていただくことにしました。ありがとうございます。
p5.jsでのお約束としてのコマンド名の書き直しや、色の変更などを行っていますが、ほぼ、元のソースそのままです。
●マンデルブロ集合 powered by p5.js(クリックすると別タブが開きます。計算が重いため画像表示までに数秒~数十秒かかる可能性があります)
コードはこちらになります。
const N = 255;
const L = 255;
const SCALE = 3.8;
function setup() {
createCanvas(600, 600);
noLoop();
}
function draw() {
translate(width / 2, height / 2);
background(0);
for (let a = -width / 2; a <= width / 2; a++) {
for (let b = -height / 2; b <= height / 2; b++) {
let x = SCALE * a / width;
let y = SCALE * b / height;
let r = calc(x, y);
stroke(r * 12 % 256, r * 4 % 256, r * 16 % 256);
rect(a, b, 1, 1);
}
}
}
function calc(x, y) {
let tx, ty;
let zx = 0.0;
let zy = 0.0;
for (let i = 1; i <= N; i++) {
tx = zx;
ty = zy;
zx = tx * tx - ty * ty + x;
zy = 2 * tx * ty + y;
if (zx * zx + zy * zy > L)
return i;
}
return 0;
}
数式は理解できなかったのですが、コードで見る限り、決して複雑怪奇な計算をしているわけではないのですね。むしろシンプル。なのに描かれる画像は有機的で美しい。「マンデルブロ集合」が高い人気を誇る理由が、なんとなく分かる気がします(式の意味わかってないけど)。
「コッホ曲線」と「ドラゴン曲線」
フラクタル画像を描くプログラムは、チュートリアルとしてもよく使われています。ちょっと調べてみたら、翔泳社さんの「CodeZine」に、こんな記事がありました。
・再帰プログラムによるフラクタル図形の描画 - Javaで学ぶグラフィックス処理(CodeZine)
こちらに掲載されていた「コッホ曲線」と「ドラゴン曲線」のJavaコードを、p5.js向けに書き直してみました。
●コッホ曲線 powered by p5.js(クリックすると別タブが開きます)
●ドラゴン曲線 powered by p5.js(クリックすると別タブが開きます)
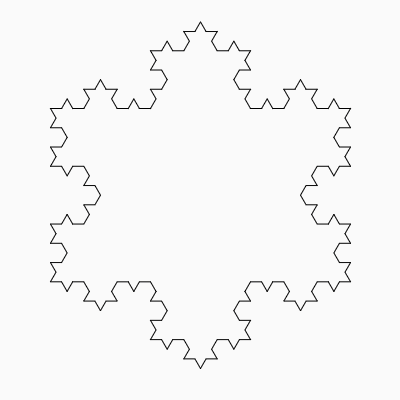
「コッホ曲線」は直線を3等分して、真ん中の線分を折れ線状に出っ張らせるという処理を、新たにできた辺も含めてすべてに対して繰り返すという再帰を行います。スタートが正三角形だと、このサンプルのような「コッホ島」あるいは「コッホ雪片」と呼ばれるような図形になります。
var REF = 2;
var P = new PointObj();
var Q = new PointObj();
var R = new PointObj();
P.x = 150; P.y = 193;
Q.x = 450; Q.y = 193;
R.x = 300; R.y = 453;
function setup() {
createCanvas(600, 600);
noLoop();
strokeWeight(1);
stroke(0);
background(250);
drawKoch(P, Q, REF);
drawKoch(Q, R, REF);
drawKoch(R, P, REF);
}
function drawKoch(a, b, n) {
var c = new PointObj();
var d = new PointObj();
var e = new PointObj();
var xx, yy;
var angle1, angle2, distance;
c.x = (2 * a.x + b.x) / 3;
c.y = (2 * a.y + b.y) / 3;
d.x = (a.x + 2 * b.x) / 3;
d.y = (a.y + 2 * b.y) / 3;
xx = b.x - a.x;
yy = -(b.y - a.y);
distance = Math.sqrt(xx * xx + yy * yy) / Math.sqrt(3);
if (xx >= 0) {
angle1 = Math.atan(yy / xx) + Math.PI / 6;
e.x = a.x + distance * Math.cos(angle1);
e.y = a.y - distance * Math.sin(angle1);
} else {
angle2 = Math.atan(yy / xx) - Math.PI / 6;
e.x = b.x + distance * Math.cos(angle2);
e.y = b.y - distance * Math.sin(angle2);
}
if (n <= 0) {
line(a.x, a.y, c.x, c.y);
line(c.x, c.y, e.x, e.y);
line(e.x, e.y, d.x, d.y);
line(d.x, d.y, b.x, b.y);
} else {
drawKoch(a, c, n - 1);
drawKoch(c, e, n - 1);
drawKoch(e, d, n - 1);
drawKoch(d, b, n - 1);
}
}
function PointObj() {
var x, y;
}
「ドラゴン曲線」も同じような感じですが、こちらは2点間に引かれた1本の直線を初期状態として、以降、すべての線分をルールに従った方向で直角に交わる2直線に変えていくという処理になります。こちらについては、18回分の再帰による変化がわかるアニメーションとして描いてみました。
var maxdraw = 18;
var count = 0;
var P = new PointObj();
var Q = new PointObj();
function setup() {
createCanvas(600, 600);
smooth();
noFill();
frameRate(1);
P.x = 250; P.y = 150;
Q.x = 450; Q.y = 450;
strokeWeight(0.5);
stroke(100, 100, 255, 255);
}
function draw() {
if (count < maxdraw) {
background(250, 250, 200);
drawDragon(P, Q, count);
count++;
} else { noLoop(); }
}
function drawDragon(a, b, n) {
var c = new PointObj();
var xx, yy;
xx = b.x - a.x;
yy = -(b.y - a.y);
c.x = a.x + (xx + yy) / 2;
c.y = b.y + (xx + yy) / 2;
if (n <= 0) {
line(a.x, a.y, c.x, c.y);
line(b.x, b.y, c.x, c.y);
} else {
drawDragon(a, c, n - 1);
drawDragon(b, c, n - 1);
}
}
function PointObj() {
var x, y;
}
フラクタルのシダ(バーンズリーのシダ)
前回まで見てきた「セル・オートマトン」にしろ、今回の「フラクタル」にしろ、自然界や現実世界にある一見複雑な構成や現象を、シンプルな数理モデルに還元できるという面白さが、僕のようなド文系をも引きつけてやまない魅力だと思うのですが「フラクタルのシダ」は、その極めつけでしょう。
フラクタルのシダについては、Wikipediaの「反復関数系」の項で計算方法が説明されています。
・反復関数系 - Wikipedia(下の方に例として「フラクタルのシダ」に関する記述)
やっていることは、ひたすら点を描画する座標を変換するという処理で、変換ルールは決まった確率で4つの中から1つが選択されるという、それだけのことです。
●フラクタルのシダ powered by p5.js(クリックすると別タブが開きます)
それだけのことなのに、徐々にできあがっていく画像はどう見ても「シダ」なんですよねぇ。理屈は知っているのに、なんで結果がそうなるのかが直感的に分からないあたりにカオスのスゴみを感じます。ちなみに、スケッチでは打つドットの色を少しずつ変えており、しばらく放っておくと、だんだん紅葉していくような感じにしてみました。
let x = 0;
let y = 0;
let c = 180;
const r = 59;
function setup() {
createCanvas(600, 600);
colorMode(HSB);
background(0);
}
function draw() {
for (let i = 0; i < 500; i++) {
let tx = 0;
let ty = 0;
stroke(c, 60, 100, .1);
point((x * r) + width / 2 - 50, height - y * r);
let sw = random(100);
if (sw > 15) {
tx = 0.85 * x + 0.04 * y;
ty = -0.04 * x + 0.85 * y + 1.6;
} else if (sw > 8) {
tx = -0.15 * x + 0.28 * y;
ty = 0.26 * x + 0.24 * y + 0.44;
} else if (sw > 1) {
tx = 0.2 * x - 0.26 * y;
ty = 0.23 * x + 0.22 * y + 1.6;
} else {
tx = 0;
ty = y * 0.16;
}
x = tx;
y = ty;
}
c -= .2;
}
「フラクタル」ネタは、次回以降もしばらく続きます。





p5.jsでなんとなくフラクタル はコメントを受け付けていません